Question

X^2 -5x + 6 = 0 I need to graph.I need 5 points for the graph.

Answer 1

Given the Quadratic Equation:

`x^2-5x+6=0`

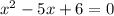
1. Find the x-intercepts:

- Factor the equation by finding two numbers whose sum is -5 and whose product is 6. These are -2 and -3, because:

`\begin{gathered} -2-3=-5 \\ (-2)(-3)=6 \end{gathered}`

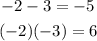
Then:

`(x-2)(x-3)=0`

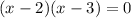
- Now you know that the x-intercepts are:

`\begin{gathered} x_1=2 \\ x_2=3 \end{gathered}`

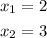
2. Now you need to graph this function:

`y=x^2-5x+6`

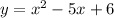
In order to find the graph with better precision, you can find the vertex:

- Find the x-coordinate with this formula:

`x=-(b)/(2a)`

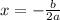
In this case, knowing that the function has the form:

`y=ax^2+bx+c`

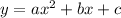
You can identify that:

`\begin{gathered} b=-5 \\ a=1 \end{gathered}`

Then, you get:

`x=-((-5))/(2(1))=(5)/(2)=2.5`

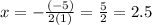
- Find the y-coordinate of the vertex by substituting the x-coordinate into the function and evaluating:

`y=(2.5)^2-5(2.5)+6=-0.25`

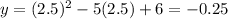
Hence, the vertex of the parabola is:

`(2.5,-0.25)`

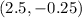
3. To find two other points on the parabola, you can substitute these values into the function and evaluate:

`\begin{gathered} x=2.2 \\ x=2.7 \end{gathered}`

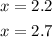
Then, you get:

`\text{For }x=2.2\rightarrow y=(2.2)^2-5(2.2)+6=-0.16`
`\text{For }x=2.7\rightarrow y=(2.7)^2-5(2.7)+6=-0.21`

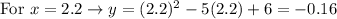
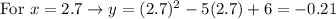
Therefore, you know these two other points:

`\mleft(2.2,-0.16\mright),\mleft(2.7,-0.21\mright)`

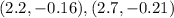
Hence, the answer is: