Question

Find the half-life of a radioactive sample, if the activity drops to 1/16 of its initial value in 80 minutes

Answer 1

`\begin{equation*} 1200\text{ seconds }=20\text{ minutes} \end{equation*}`

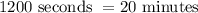
Step-by-step explanation

To calculate the half-life of the sample, apply the formula for the quantity remaining in a radioactive decay:

`(N)/(N_o)=((1)/(2))^n`

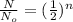
where N/No = ratio of quantity remaining to initial quantity = 1/16

and n is:

`n=\frac{T}{t_{(1)/(2)}}`

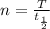
where T = time elapsed = 80 mins = 4800 seconds

t1/2 = half-life

Solving for n in the equation above:

`\begin{gathered} (1)/(16)=((1)/(2))^n \\ \\ ((1)/(2))^4=((1)/(2))^n \\ \\ \Rightarrow n=4 \end{gathered}`

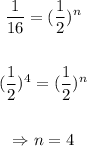
Therefore, the half-life of the sample is:

`\begin{gathered} 4=\frac{4800}{t_{(1)/(2)}} \\ \\ t_{(1)/(2)}=(4800)/(4) \\ \\ t_{(1)/(2)}=1200\text{ seconds }=20\text{ minutes} \end{gathered}`

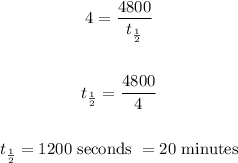
That is the answer.