Question

Suppose a house that costs $270,000 appreciates by 5% each year.

In about how many years will the house be worth $350,000? Use the equation 350 = (270)(1.05)x and round the value of x to the nearest year

Answer 1

THE ANSWER TO YOUR PROBLEM IS 5 I HOPED I COULD HELP

Answer 2

6 years.

Explanation:

We have been given that a house that costs $270,000 appreciates by 5% each year. We are asked to find the number of years it will take the house to be worth 350,000 by using equation
`350=270*(1.05)^x`.

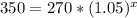First of all let us divide both sides of our equation by 270.

`(350)/(270)=(270*(1.05)^x)/(270)`

`(350)/(270)=(1.05)^x`

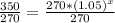
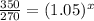
Upon taking natural log of both sides of our equation we will get,

`ln((35)/(27))=ln((1.05)^x)`

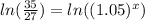
Using natural log property
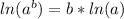`ln(a^b)=b*ln(a)` we will get,

`ln((35)/(27))=x*ln(1.05)`

`0.2595111954850846=x*0.048790164169432`

`x=(0.2595111954850846)/(0.048790164169432)`

`x=5.31892441648`

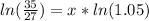
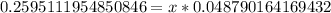
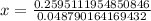
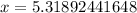
Since it will take more time than 5 years, so will round up our answer.

`x\approx 6`

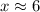
Therefore, in approximately 6 years the house will be worth $350,000.