Question

Determine the center and radius of the following circle equation:x2 + y2 + 4x – 10y + 13 = 0

Answer 1

The general equation of a circle is given in the form:

`\begin{gathered} (x-a)^2+(y-b)^2=r^2 \\ \text{where} \\ a,b\text{ are the center of the circle} \\ r\text{ is the radius of the circle} \end{gathered}`

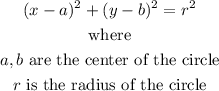
Therefore to go about this, we will follow the steps below

Step 1: write out the equation

`x^2+y^2+4x-10y+13=0`

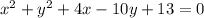
Step 2: Re-goup and apply completing the square method

`x^2+4x+y^2-10y=0-13`

=>

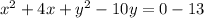
Completeing the square:

`\begin{gathered} (x+2)^2-4+(y-5)^2-25=0-13 \\ (x+2)^2+(y-5)^2=0-13+4+25 \end{gathered}`

=>

`(x+2)^2+(y-5)^2=16`

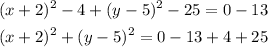
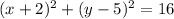
Step 3: Re-write the equation to conform to the general equation

This will give:

`(x+2)^2+(y-5)^2=4^2`

Upon comparing this with the general equation

`\begin{gathered} a=-2 \\ b=5 \\ r=4 \end{gathered}`

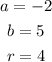
Therefore,

The center = -2, 5

radius = 4