To answer this question, we need to remember was the discriminant of a quadratic equation means. The discriminant is given by the following formula:

The values of a, b, and c, are:
• a is the leading coefficient (or quadratic coefficient)
,
• b is the linear coefficient
,
• c is the constant-coefficient
We can see this in the general formula:
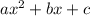
In this case, we have that the polynomial:
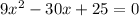
Then
• a = 9
,
• b = -30
,
• c = 25
If we use the formula of the discriminant, we have:
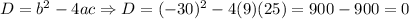
When we have that the discriminant of the polynomial is equal to 0, then the parabola that represents the quadratic formula will have only one x-intercept. It has one real solution. However, this solution is a multiplicity, that is this solution is