Question

Differentiate. f(x) = (x3 - 8)2/3 O f'(x) 2x 3 Vx3-8 O f'(x) = S 2x2 f(x) = 3 Vx3-5 O x2 f'(x) 3 Nx3-S

Answer 1

According to the given data we have the following expression:

`f(x)=\mleft(x^3-8\mright)^{(2)/(3)}`

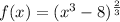
To find f'(x) we would have to make the following calculation:

First:

Apply the chain rule

So:

`\mathrm{Apply\: the\: chain\: rule}\colon(d)/(dx)\mleft(\mleft(x^3-8\mright)^{(2)/(3)}\mright)=\quad \frac{2}{3\left(x^3-8\right)^{(1)/(3)}}(d)/(dx)\mleft(x^3-8\mright)`
`(d)/(dx)\mleft(x^3-8\mright)=3x^2`

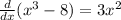
So:

`\frac{2}{3\left(x^3-8\right)^{(1)/(3)}}(d)/(dx)\mleft(x^3-8\mright)=\frac{2}{3\left(x^3-8\right)^{(1)/(3)}}\cdot\: 3x^2`

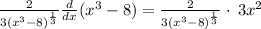
Next, you would have to simplify the expression above:

`\mathrm{Simplify\: }\frac{2}{3\left(x^3-8\right)^{(1)/(3)}}\cdot\: 3x^2=\quad \frac{2x^2}{\left(x^3-8\right)^{(1)/(3)}}`

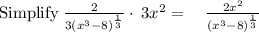
Therefore:

`\frac{2x^2}{\left(x^3-8\right)^{(1)/(3)}}=\frac{2x^2}{\sqrt[3]{x^3}^{}-8}`

Therefore, the right answer is

`f^(\prime)(x)=\frac{2x^2}{\sqrt[3]{x^3}^{}-8}`