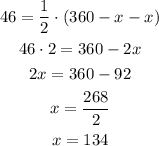Question

you focus your camera on a circular Fountain your camera is at the vertex of the angle formed by tangents to the Fountain you estimate that the angle is 46 degrees .what is the measure of the arc of the circular basin of the fountain that will be in the photograph ? The measure of the arc of the circular basin of the fountain that Will be in the photograph is _° (Simplify your answer .)

Answer 1

The measure of the arc of the circular is 134°

Explanation:

We have that the measure of an angle formed when two lines intersect outside a circle is half the difference of the measure of the intercepted arcs, therefore

`\begin{gathered} \alpha=(1)/(2)\cdot(\Theta-\theta) \\ \Theta=\text{ big angle} \\ \theta=\text{ small angle} \\ \alpha=46\text{\degree} \\ \Theta=360-x \\ \theta=x \end{gathered}`

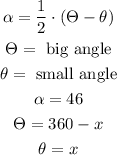
Replacing and solving for x:

`\begin{gathered} 46=(1)/(2)\cdot(360-x-x) \\ 46\cdot2=360-2x \\ 2x=360-92 \\ x=(268)/(2) \\ x=134\text{\degree} \end{gathered}`