Answer : The value of
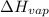 is 47.627 kJ/mol
is 47.627 kJ/mol
Explanation :
To calculate
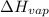 of the reaction, we use clausius claypron equation, which is:
of the reaction, we use clausius claypron equation, which is:
![\ln((P_2)/(P_1))=(\Delta H_(vap))/(R)[(1)/(T_1)-(1)/(T_2)]](https://img.qammunity.org/2018/formulas/chemistry/college/6alp85vylfoeieczpwbqk54ydvsny0q7dv.png)
where,
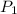 = vapor pressure at temperature
= vapor pressure at temperature
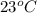 = 92 torr
= 92 torr
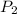 = vapor pressure at temperature
= vapor pressure at temperature
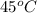 = 351 torr
= 351 torr
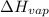 = Enthalpy of vaporization = ?
= Enthalpy of vaporization = ?
R = Gas constant = 8.314 J/mol K
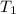 = initial temperature =
= initial temperature =
![23^oC=[23+2730]K=296K](https://img.qammunity.org/2018/formulas/chemistry/college/g52jnjbt6thn8v8hpw89omllz61gcn22rd.png)
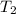 = final temperature =
= final temperature =
![45^oC=[45+2730]K=318K](https://img.qammunity.org/2018/formulas/chemistry/college/j5xek2cbeax28zris94a6jscgpylr3bdpp.png)
Putting values in above equation, we get:
![\ln((351torr)/(92torr))=(\Delta H_(vap))/(8.314J/mol.K)[(1)/(296)-(1)/(318)]\\\\\Delta H_(vap)=47627.347J/mol=47.627kJ/mol](https://img.qammunity.org/2018/formulas/chemistry/college/tnkbgckd1f28uijwmqu01qy6wurxrhu3gq.png)
Therefore, the value of
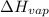 is 47.627 kJ/mol
is 47.627 kJ/mol