A. Solve the differential equation y'=2x √(1-y^2). b. Explain why the initial value problem y'=2x √(1-y^2) with y(0) = 3 does not have a solution.

Question

A. Solve the differential equation
`y'=2x √(1-y^2)`.

b. Explain why the initial value problem
`y'=2x √(1-y^2)` with y(0) = 3 does not have a solution.

Answer 1

`y' = (dy)/(dx)`

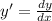
seperable differential equations will have the form

`(dy)/(dx) = F(x) G(y)`

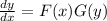
what you do from here is isolate all the y terms on one side and all the X terms on the other

`(dy)/(G(y)) = F(x) dx`
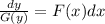
just divided G(y) to both sides and multiply dx to both sides

then integrate both sides

`\int (1)/(G(y)) dy = \int F(x) dx`

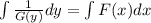
once you integrate, you will have a constant. use the initial value condition to solve for the constant, then try to isolate x or y if the question asks for it


In your problem,

`G(y) = √(1-y^2) F(x) = 2x`

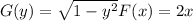
so all you need to integrate is

`\int (1)/(√(1-y^2)) dy = \int 2x dx`