Question

What are the period and phase shift for f(x) = 5 tan(2x − π)?

Period: π; phase shift: x = pi over two
Period: π; phase shift: x = negative pi over two
Period: pi over two; phase shift: x = negative pi over two
Period: pi over two; phase shift: x = pi over two
I think it is A.. Please explain

Answer 1

period: pi/2; phase shift: x = -pi/2

Answer 2

D.
`\text{Period}=(\pi)/(2)`; Phase shift
`x=(\pi)/(2)`

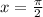
Explanation:

We have been given a function
`f(x)=5\text{ tan}(2x-\pi)`. We are asked to find the period and phase shift for the given function.

We will use formula
`f(x)=a\cdot \text{tan}(bx-c)+d`, where,

a = Amplitude,

`\text{Period}=(\pi)/(|b|)`

`\text{Phase shift}=(c)/(b)`

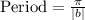
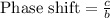
d = Vertical shift.

Upon substituting the given values we will get period of the given function as:

`\text{Period}=(\pi)/(|2|)=(\pi)/(2)`

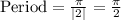
We can find phase shift for our given function as:

`x=(\pi)/(2)`

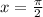
Therefore, option D is the correct choice.