Question

If the endpoints of the diameter of a circle are (−6, 6) and (6, −2), what is the standard form equation of the circle?

Answer 1

i Acehello :
let : A(-6,6) B(6,-2)
the center is w((-6+6)/2 , (6-2)/2)....(midel [ AB]
w(0 ,2)
the ridus is : r = AB/2
AB = √(-6-6)²+(6+2)² = √(144+64) =√208/2
an equation in standard form equation of the circle :
(x+0)²+(y-2)² = (√208/2)²=208/4 = 52

Answer 2

Hence, equation of circle is:

`x^2+y^2-4y=48`

Explanation:

Te end points of the diameter are given to be:

(−6, 6) and (6, −2).

We know that the center of the circle is the mid-point of the diameter.

and the coordinates of the mid-point (e,f) of (a,b) and (c,d) is calculated as:

`e=(a+c)/(2), f=(b+d)/(2)`

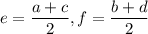
Here we have (a,b)=(-6,6) and (c,d)=(6,-2).

Hence, the coordinates of center (e,f) is calculated as:

`e=(-6+6)/(2),f=(6-2)/(2)\\\\e=(0)/(2),f=(4)/(2)\\\\e=0,f=2`

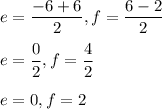
Hence, center is located at: (0,2)

Now, the radius of circle is the the distance between the center and a point on the circle.

i.e. distance between (0,2) and (6,-2).

We know that the distance between two points (a,b) and (c,d) is calculated as:

`=√((c-a)^2+(d-b)^2)`

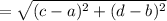
Here we have (a,b)=(0,2) and (c,d)=(6,-2)

Hence, the length of the radius is calculated as:

`√((6-0)^2+(-2-2)^2)\\\\=√(36+16)\\\\=√(52)\\\\=2√(13)`

Hence, the equation of the circle with center (h,k) and radius r is given by:

`(x-h)^2+(y-k)^2=r^2`

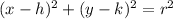
Hence, the equation of circle is:

`(x-0)^2+(y-2)^2=(2√(13))^2\\\\x^2+y^2+4-4y=52\\\\x^2+y^2-4y=48`

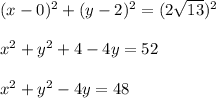
Hence, equation of circle is:

`x^2+y^2-4y=48`