Question

The Bear Lake in Idaho is 24 miles long. Suppose John starts cycling at one end at 20 miles per hour and Ramona starts at the other end at 16 miles per hour. How long would it take them to meet?

Answer 1

We have a distance between John and Ramona that is d = 24 miles.

We can graph this situation as:

They will meet at the same point and at the same time.

If we call x the length travelled by John to the meeting point, Ramona would have travelled (24 - x) miles.

As the time is the same for both, we can express the time as the distance travelled divided by the speed of each one:

`\begin{gathered} t=(d_(john))/(v_(john))=(d_(ramona))/(v_(ramona)) \\ (x)/(20)=(24-x)/(16) \end{gathered}`

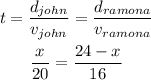
We can now solve for x as:

`\begin{gathered} (x)/(20)=(24-x)/(16) \\ 16x=20(24-x) \\ 4x=5(24-x) \\ 4x=120-5x \\ 4x+5x=120 \\ 9x=120 \\ x=(120)/(9) \\ x=(40)/(3) \end{gathered}`

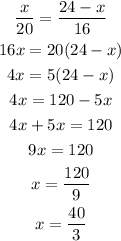
Then, they will meet 40/3 miles from the point where John starts.

As we want to calculate the time, we can use the distance x and the speed of John to calculate the time:

`t=(x)/(v)=((40)/(3))/(20)=(2)/(3)\text{ hours}`

We can convert this to minutes to have an exact value:

`t=(2)/(3)\text{ hours}*\frac{60\text{ min}}{1\text{ hour}}=40\text{ min}`

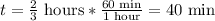
Answer: they will meet after 40 minutes.