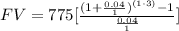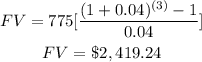Question

Michael wants to save money for his daughters graduation gift. He deposits $775 at the end of each year in an ordinary annuity that pays 4% interest, compounded annually.

Answer 1

we have that

The formula for the future value of an ordinary annuity is equal to:

`FV=P\lbrack((1+ (r)/(n) )^(nt) -1)/( (r)/(n) )\rbrack`

where

FV is the future value

P is the periodic payment

r is the interest rate in decimal form

n is the number of times the interest is compounded per year

t is the number of years

In this problem we have

P=$775

n=1

r=4%=0.04

Part a

t=1 year

substitute

`FV=775\lbrack((1+(0.04)/(1))^((1\cdot1))-1)/((0.04)/(1))\rbrack`

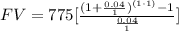
simplify

`\begin{gathered} FV=775\lbrack((1+0.04)^1-1)/(0.04)\rbrack \\ FV=\$775 \end{gathered}`

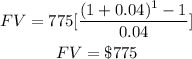
For the first year is the same amount

Part b

For t=2 years

`FV=775\lbrack((1+(0.04)/(1))^((1\cdot2))-1)/((0.04)/(1))\rbrack`
`\begin{gathered} FV=775\lbrack((1+0.04)^((1\cdot2))-1)/(0.04)\rbrack \\ FV=\$1,581 \end{gathered}`

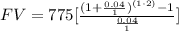
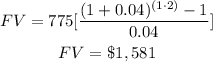
Part c

For t=3 years

`FV=775\lbrack((1+(0.04)/(1))^((1\cdot3))-1)/((0.04)/(1))\rbrack`
`\begin{gathered} FV=775\lbrack((1+0.04)^((3))-1)/(0.04)\rbrack \\ FV=\$2,419.24 \end{gathered}`