Question

Monochromatic light passes through two narrow slits 0.23 mm apart and forms an interference pattern on a screen 2.13 m away. If light of wavelength 645.78 nm is used, what is the distance from the center of the central maximum to the center of the third order bright fringe in centimeters?

Answer 1

Given:

The distance between the two narrow slits is

`\begin{gathered} d=\text{ 0.23 mm} \\ =2.3*10^(-4)\text{ m} \end{gathered}`

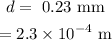
The distance between the slit and the screen is

`D=\text{ 2.13 m}`

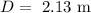
The wavelength of the light is

`\begin{gathered} \lambda\text{ = 645.78 nm} \\ =645.78*10^(-9)\text{ m} \end{gathered}`

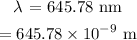
Required: Distance of the third bright fringe from the central maximum.

Step-by-step explanation:

The third bright fringe will have m = 3.

The distance of the third bright fringe from the central maximum can be calculated by the formula

`y=\frac{m\lambda\text{ D}}{d}`

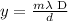
On substituting the values, the distance can be calculated as

`\begin{gathered} y=(3*645.78*10^(-9)*2.13)/(2.3*10^(-4)) \\ =0.0179\text{ m} \end{gathered}`

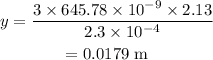
Final Answer: The distance of the third bright fringe from the central maximum is 0.0179 m.