Recall the definition of the floor function: if

is an integer and

, then
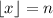
. So
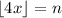
iff
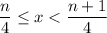
.
So let's consider four case.
First, suppose
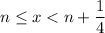
where
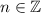
. It follows that
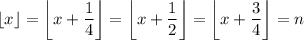
because at most, we have
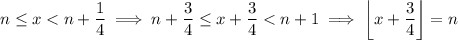
Meanwhile,
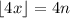
, which follows immediately from

and so

Then for the second case, you can consider what happens when you have

; for the third,
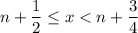
; and for the fourth,
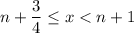
.