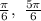Let's determine the solutions of the following:
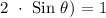
We get,
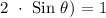
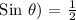

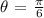
Since we are asked for the solution at 0 < Θ < 2π interval, we will be looking at the solution in the 1st and second quadrants.
For the second solution, subtract the reference angle from π to find the solution in the second quadrant.
We get,

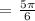
Therefore, the solutions are: