Question

At the beginning of each year for 14 years, Sherry Kardell invested $400 that earns 10% annually. What is the future value of Sherry's account in 14 years?

Answer 1

hmm if I'm not mistaken, is just an "ordinary" annuity, thus


`\bf \qquad \qquad \textit{Future Value of an ordinary annuity} \\\\ A=pymnt\left[ \cfrac{\left( 1+(r)/(n) \right)^(nt)-1}{(r)/(n)} \right] \\\\\\`


`\bf \begin{cases} A= \begin{array}{llll} \textit{original amount}\\ \textit{already compounded} \end{array} & \begin{array}{llll} \end{array}\\ pymnt=\textit{periodic payments}\to &400\\ r=rate\to 10\%\to (10)/(100)\to &0.1\\ n= \begin{array}{llll} \textit{times it compounds per year}\\ \textit{annually, so once} \end{array}\to &1\\ t=years\to &14 \end{cases} \\\\\\ A=400\left[ \cfrac{\left( 1+(0.1)/(1) \right)^(1\cdot 14)-1}{(0.1)/(1)} \right]`

Answer 2

Dependent on which interest plan. On simple interest Sherry Kardell will have a future value of $960 in her account.

Explanation:

The simple interest is defined as:

`A=P*(1+r*t)`

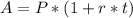
A is the future amount of money after interest. P is the principal money that is being invested. t is the time that the money is invested and r is that interest rate the money invested to.

P = $400, r=0.1, t=14 years

`A=400*(1+0.1*14)=960`

Therefore she will have 960-400=$560 more in her account after 14 years.