ANSWER
x = 2.9, y = -1.6 and x = -1.7, y = 6.7
Step-by-step explanation
We are given two equations:
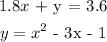
From the first equation, we have:
y = 3.6 - 1.8x
Put that in the second, we have:
![\begin{gathered} 3.6-1.8x=x^2\text{ - 3x - 1} \\ \text{Collect like terms:} \\ x^2\text{ - 3x - 1 - 3.6 + 1.8x = 0} \\ x^2-\text{ 1.2x - 4.6 = 0} \\ U\sin g\text{ quadratic formula:} \\ x\text{ = }\frac{-b\text{ }\pm\sqrt[]{b^2-4ac}}{2a} \\ \text{where a = 1, b = -1.2, c = -4.6} \\ \Rightarrow\text{ x = }\frac{1.2\text{ }\pm\sqrt[]{(-1.2)^2\text{ - 4(1)(-4.6)}}}{2}\text{ = }\frac{1.2\text{ }\pm\sqrt[]{1.44\text{ + 18.4}}}{2} \\ x\text{ = }\frac{1.2\text{ }\pm\text{ }\sqrt[]{19.84}}{2}\text{ } \\ x\text{ = }\frac{1.2\text{ +4.5}}{2}\text{ and x = }\frac{1.2\text{ - 4.5}}{2} \\ x\text{ = }(5.7)/(2)\text{ and x = }(-3.3)/(2) \\ x\text{ }\cong2.9\text{ and -1.7} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/t2g1d6l2xspnxkditszn.png)
Put each of those values of x in the first equation:
y = 3.6 - 1.8(2.9) and y = 3.6 - 1.8(-1.7)
y = 3.6 - 5.22 and y = 3.6 + 3.06
y = -1.6 and y = 6.7 (approximately to the nearest tenth)
Therefore, the solutions are:
x = 2.9, -1.6 and x = -1.7, y = 6.7