2 Answers

Alexander Finn · Answer 1 · 2018-10-10T04:41:54+0000

Answer:

Option A and Option B are not equivalent to the given expression.

Explanation:

We are given the following expression:

$4^{(2)/(3)}$

Applying properties of exponents and base:

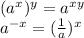
$(a^x)^y = a^(xy)\\a^(-x)= ((1)/(a))^x\\$

A. Using the exponential property
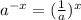$a^(-x)= ((1)/(a))^x\\$ , we can write:

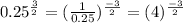
$0.25^{(3)/(2)} = ((1)/(0.25))^{(-3)/(2)} = (4)^{(-3)/(2)}$

which is not equal to the given expression.

B. Using the exponential property
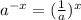$a^(-x)= ((1)/(a))^x\\$ , we can write:

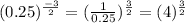
$(0.25)^{(-3)/(2)} = ((1)/(0.25))^{(3)/(2)} = (4)^{(3)/(2)}$

which is not equal to the given expression.

C. First we convert the radical form into exponent form. Then by using the property
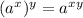(a^x)^y = a^(xy) of exponent, we can write the following:

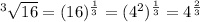
$^3√(16) = (16)^{(1)/(3)} = (4^2)^{(1)/(3)} = 4^{(2)/(3)}$

which is equal to the given expression.

D. First we convert the radical form into exponent form. Then by using the property
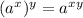(a^x)^y = a^(xy) of exponent, we can write the following:

$(^3√(4))^2 = (4^{(1)/(3)})^2 = 4^{(2)/(3)}$

which is equal to the given expression.

Option D and Option C are equivalent to the given expression.

Please log in or register to add a comment.