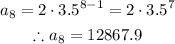Question

1.The graph shows the first three terms in a geometric sequence. (a)What is the common ratio r? Explain or show how you determined your answer.(b)What is the recursive formula for the sequence?(c)What is the iterative formula for the sequence?(d)Show how to use your answer from Part (c) to find the eighth term of the sequence. Round your answer to the nearest tenth.

Answer 1

Looking at the graph, the three consecutive elements of the sequence are:

`2,7,24.5`

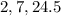
(a)

The common ratio r is the division between two consecutive elements, with the n-th element as the denominator and the (n+1)-th element as the numerator. From the list of elements, the common ratio is:

`r=(7)/(2)=(24.5)/(7)=3.5`

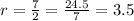
(b)

The initial value of the sequence is 2, and the common ratio is 3.5, The general recursive formula can be expressed as:

`\begin{gathered} a_1=b \\ a_(n+1)=a_n\cdot r,\text{ for }n\ge1 \end{gathered}`

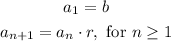
Now, for our problem, we identify b = 2 and r = 3.5. The recursive formula is:

`\begin{gathered} a_1=2 \\ a_(n+1)=3.5\cdot a_n,\text{ for }n\ge1 \end{gathered}`

( )

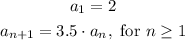
The explicit formula of the sequence is:

`a_n=a_1\cdot r^(n-1),\text{ for }n\ge1`

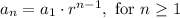
Using the values of a₁ and r:

`a_n=2\cdot3.5^(n-1),\text{ for }n\ge1`

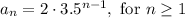
(d)

The eighth term of the sequence can be calculated if we set n = 8 in the previous formula:

`\begin{gathered} a_8=2\cdot3.5^(8-1)=2\cdot3.5^7 \\ \therefore a_8=12867.9 \end{gathered}`