Question

A circle has a 6 centimeter radius and a shaded sector with a central angle of60°. Determine the area of the shaded sector.The shaded sector is [a] cm2.

Answer 1

The circle with a radius of 6cm and a sector with a central angle measuring 60 degrees is sketched above. Note that the shaded sector that is bounded by two radii is shaded in peach color.

The area of a circle is derived as

`A=\pi* r^2`

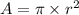
Therefore, the area of a sector (cut out of a complete 360 degree circle) is derived as a fraction of the area of a circle. The central angle of the sector will be used to determine the "fraction" of the area as shown below;

`\begin{gathered} \text{Area of a sector=}(\theta)/(360)*\pi* r^2 \\ \text{Where, }\theta=the\text{ central angle of the sector} \\ r=\text{radius, }\pi=3.14 \end{gathered}`

Pi is usually given as 3.14, except the question gives you another specific and different value. The solution now is;

`\begin{gathered} \text{Area of shaded sector=}(60)/(360)*3.14*6^2 \\ \text{Area of shaded sector=}(60)/(360)*3.14*36 \\ \text{Area}=(60*3.14*36)/(360) \\ \text{Area}=(6782.4)/(360) \\ \text{Area}=18.84cm^2 \end{gathered}`