We are given the following information.
Mean = 81
Standard deviation = 8
We are asked to find the probability that a randomly chosen score will be greater than 93.
Recall that the z-score is given by
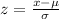
Where μ is the mean, σ is the standard deviation, and x is the raw score.
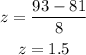
So, the z-score is 1.5
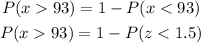
From the z-table, the probability corresponding to the z = 1.5 is found to be 0.93319
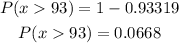
There is a 0.0668 probability that a randomly chosen score will be greater than 93.