a) the slope is 250
b)for every mile ( along thail) the hikers progress 250 meters ( elevation)
c)y=250x+500
3d)yes, the equation y-250x=500 represents the same relationship
Step-by-step explanation
Step 1
slope of the line.
the slope of a line is given by the expression

then
pick up two poins from the line
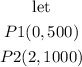
replace in the expression
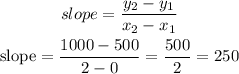
so, the slope is 250
Step 2
what does the slope tell use about this situation
as the slope is rate of change
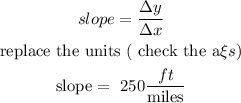
so, the slope tell us
for every mile ( along thail) the hikers progress 250 meters ( elevation)
Step 3
equation:
to find the equation we can use the point slope equation
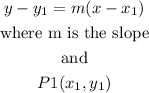
replace
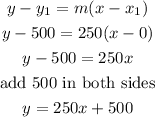
Step 4
finally.
Does the equation y-250x=500 represent the same relationship?
if we start from

then, we apply the subtraction property of equality ( which does not affect the function)
so
subtract 250 x in both sides
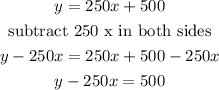
so
yes, the equation y-250x=500 represents the same relationship
I hope this helps you