Question

Is my answer, right?

The table of values represents a polynomial function f(x). How much greater is the average rate of change over the interval [7, 9] than the interval [4, 6]?
x f(x)
4 105
5 384
6 945
7 1,920
8 3,465
9 5,760

Is the answer 605 or am I way off?? $.$

Answer 1

to the the average rate of change of (7,9), you would do f(9)-f(7) all over 9-7, which comes out to be 1920, do the same thing over (4,6) and you get 420. So your answer is 1500.

Answer 2

The average rate of change A(x) over interval [a, b] is given by:

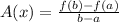`A(x) = (f(b)-f(a))/(b-a)` .....[1]

As per the statement:

The table of values represents a polynomial function f(x).

For interval [7, 9]

f(7) = 1920

f(9) = 5760

then

using equation [1] we have;

`A_1(x) = (f(9)-f(7))/(9-7)`

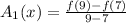
Substitute the given values we have;

`A_1(x) = (5760-1920)/(9-7)=(3840)/(2)=1920`

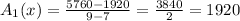
Next:

For interval [4, 6]

f(4) =105

f(6) =945

then

using equation [1] we have;

`A_2(x) = (f(6)-f(4))/(6-4)`

Substitute the given values we have;

`A_2(x) = (945-105)/(6-4)=(840)/(2)=420`

⇒
`A_1(x)-A_2(x) = 1920-420=1500`

⇒
`A_1(x) = 1500+A_2(x)`

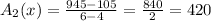
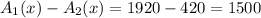
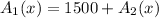
Therefore,1500 greater is the average rate of change over the interval [7, 9] than the interval [4, 6]