Question

Find the rate of change of the distance from the origin of a moving point on the graph

Answer 1

EXPLANATION

Given the function f(x) = x^2 and the point x=2

Now, we need a formula for the Distance as follows:

`(dD)/(dt)=((dD)/(dx))\cdot(\frac{dx}{d\text{ t}})`

We need to compute dD/dx, this means the derivative of the distance between the points (0,0) and (2,x^2) .

The distance must be computed using the distance formula:

`D=\sqrt[]{(x-0)^2+(x^2-0)^2}`

Adding terms and computing the powers:

`D=\sqrt[]{x^2+x^4}`

Rearranging terms:

`D=(x^4+x^2)^{(1)/(2)}`

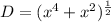
Then, we must apply the first derivative of this expression by applying the chain rule as follows:

`(df(u))/(dx)=(df)/(du)\cdot(du)/(dx)`
`f=u^{(1)/(2)},\text{ u=}x^4+x^2`
`=(d)/(du)\mleft(u^{(1)/(2)}\mright)(d)/(dx)\mleft(x^4+x^2\mright)`
`=\frac{1}{2u^{(1)/(2)}}(d)/(dx)\mleft(x^4+x^2\mright)`
`\mathrm{Substitute\: back}\: u=x^4+x^2`
`=\frac{1}{2\left(x^4+x^2\right)^{(1)/(2)}}(d)/(dx)\mleft(x^4+x^2\mright)`

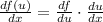
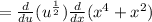
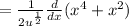
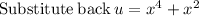
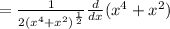
Applying the derivatives:

`=\frac{1}{2\left(x^4+x^2\right)^{(1)/(2)}}\mleft(4x^3+2x\mright)`

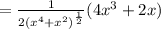
Simplifying:

`=\frac{2x^2+1}{\left(x^2+1\right)^{(1)/(2)}}`

Plugging in x=2 into the expression:

`\frac{dD}{d\text{x}}_((2))=\frac{2*2^2+1}{(2^2+1)^{(1)/(2)}}=\frac{2*4+1}{(4+1)^{(1)/(2)}}=\frac{8+1}{(5)^{(1)/(2)}}=\frac{9}{\sqrt[]{5}}`

Finally, as we already know that dx/dt = 7, we must replace terms in the expression:

`(dD)/(dt)=((dD)/(dx))\cdot(\frac{dx}{d\text{ t}})`
`\frac{dD}{d\text{ t}}=\frac{9}{\sqrt[]{5}}\cdot7`

Multiplying numbers:

`\frac{dD}{d\text{ t}}=\frac{63}{\sqrt[]{5}}=\frac{63\sqrt[]{5}}{5}=28.17`

The solution is 28.17