Question

Plot three points for the line and graph the line. Points (-4, 2)slope -4/3

Answer 1

The provisional equation of the line with slope -4/3 that passes through the point (-4,2) is:

`y\text{ = -}(4)/(3)x+b`

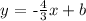
to find b, we can replace in the previous equation, the coordinates of any point of the line and solve for b. For example, we can take the point (x,y)=(-4,2) and we obtain the following equation:

`2\text{ = -}(4)/(3)(-4)+b`

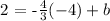
solving for b, we get:

`b\text{ = -}(10)/(3)`

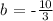
thus, the equation of the line is:

`y\text{ = -}(4)/(3)x-(10)/(3)`

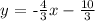
in function notation, this is equivalent to:

`f(x)\text{ = -}(4)/(3)x-(10)/(3)`

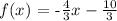
If we graph this function, we obtain the graph of the line:

and, to obtain three points on the line, we can use the formula of the line like this:

for x = 1, then:

`y=f(1)\text{ = -}(4)/(3)-(10)/(3)=-(14)/(3)`

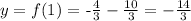
and we obtain the point :

`C=(x,y)=(1,-(14)/(3))`

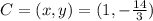
for x = 2, then:

`y=f(2)\text{ = -}(4)/(3)(2)-(10)/(3)=-6`

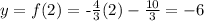
and we obtain the point :

`A=(x,y)=(2,-6)`

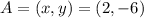
for x = 3, then:

`y=f(3)\text{ = -}(4)/(3)(3)-(10)/(3)=-(22)/(3)`

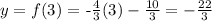
and we obtain the point :

`B=(x,y)=\text{ (3,-}(22)/(3)\text{)}`

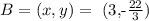
the plot of these three points on the line is: