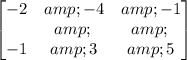Question

I need help with part "d" and "e" on this question. I have included the answers to parts "a-c" for your convenience. Is anyone available to assist on this pre-calc question? Thanks!

Answer 1

d)

Given:

`Let\text{ X}=\begin{bmatrix}{2} & {4} & {1} \\ {} & {} & {} \\ {-1} & {3} & {5}\end{bmatrix}`

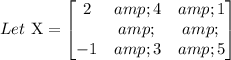
Required:

We need to rotate the triangle by 270 degrees.

Step-by-step explanation:

When rotating a point 270 degrees counterclockwise about the origin our point A(x,y) becomes A'(y, -x). This means, we switch x and y and make x negative.

Switch the first and second row of the given matrix and multiply the first row by (-1).

`\text{X'}=\begin{bmatrix}{-1} & {3} & {5} \\ {} & {} & {} \\ 2 & {4} & 1\end{bmatrix}R_1\leftrightarrow R_{2\text{ }}`

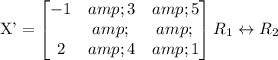
Multiply the first row by (-1).

`\text{X'}=\begin{bmatrix}{1} & -{3} & -{5} \\ {} & {} & {} \\ 2 & {4} & 1\end{bmatrix}`

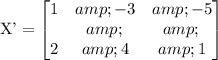
Answer:

The vertices of the image of the traignle ABC is

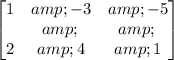
`\begin{bmatrix}{1} & -{3} & -{5} \\ {} & {} & {} \\ 2 & {4} & 1\end{bmatrix}`

e)

Given:

`Let\text{ X}=\begin{bmatrix}{2} & {4} & {1} \\ {} & {} & {} \\ {-1} & {3} & {5}\end{bmatrix}`

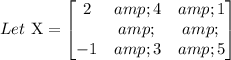
Required:

We need to reflect the triangle across the y-axis.

Step-by-step explanation:

When we reflect a point across the y-axis our point A(x,y) becomes A'(x,-y).

This means making a negative of x.

Multiply the first row by (-1).

`\begin{bmatrix}{-2} & {-4} & {-1} \\ {} & {} & {} \\ -{1} & {3} & {5}\end{bmatrix}`

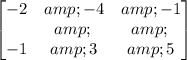
Answer:

The vertices of the image of the traignle ABC is

`\begin{bmatrix}{-2} & {-4} & {-1} \\ {} & {} & {} \\ -{1} & {3} & {5}\end{bmatrix}`