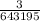A face card is a card that is a King, a Queen or a Jack. In a standard deck, there is a total of 12 face cards.
Suppose that the first 7 cards we take are faces and the remaining two are not.
The probability of taking a face on the first withdrawal, is 12/52, since there are 12 faces and there is a total of 52 cards.
On the second withdrawal, there are 11 faces remaining, and a total of 51 cards remain. Therefore, the probability of the second card also being a face is 11/51.
On the third withdrawal, the probability of taking a face will be 10/50, and so on:
On the fourth withdrawal, the probability will be 9/49.
On the fifth, 8/48.
On the sixth, 7/47.
On the seventh, 6/46.
The next two withdrawals must not be faces. On the eight withdrawal, a total of 45 cards remain, 5 of them are faces. So, the probability of not taking a face, is 40/45.
On the nineth withdrawal, the probability of not taking a face is 39/44.
The combined probability of all this events happening one after another is the product of the individual probabilities. Therefore, the probability of the hand containing exactly 7 face cards, is:
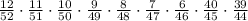
Write each factor as a product of powers of prime numbers:

Use the laws of exponents to reduce this expression:
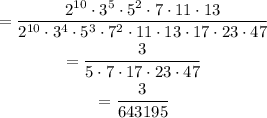
Therefore, the probability is: