Question

A state vector X for a four-state Markov chain is such that the system is four times as likely to be in state 2 as in 4, is not in state 3, and is in state 1 with probability 0.2. Find the state vector. Can someone tell me what the answer is please? I've literally tried this 40+ times and my homework says its wrong. It would be greatly appreciated.

Answer 1

All the components in the state vector need to sum to 1. You're given that component corresponding to state 1 is 0.2, and that the component for state 3 is 0.

That leaves states 2 and 4, for which you're told that the component for state 2 is four times as large. If
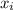
`x_i` is the component for state
`i`, then you have


`x_1+x_2+x_3+x_4=1\iff 0.2+4x_4+0+x_4=1\implies5x_4=0.8\implies x_4=0.16`

which means
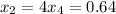
`x_2=4x_4=0.64`. So the state vector is
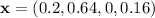
`\mathbf x=(0.2,0.64,0,0.16)`.