Let w represents the weight of the body, and let d represent the distance from the center of the earth.
Since it is given that weight varies inversely as the square of the distance, it follows that:
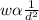
Introduce a constant k to convert the variation to an equation:
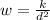
It is given that w=121 when d=3960, substitute these values into the equation and solve for k:
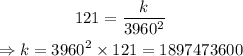
Substitute the value of the constant back into the equation:
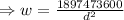
It is required to find her weight when she is 4.5 miles above sea level.
Note that at sea level, the distance to the center of the earth is 3960 miles, hence, the distance from the center of the earth to 4.5 miles above sea level is:
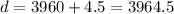
Hence, substitute d=3964.5 into the equation:
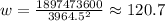
The approximate weight is 120.7 pounds.