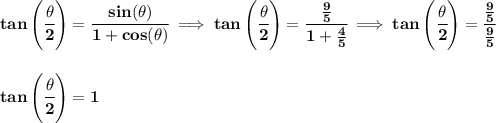well, the pythagorean theorem, gives us the +/- versions, so, which one is it?
well, our angle is at
0° < θ < 90°, meaning the 1st quadrant, and there, the opposite side, or "y" or "b", is positive, so is b = 9 then
now
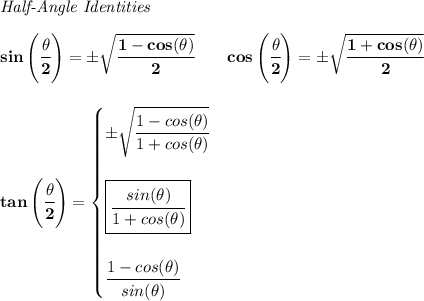
thus
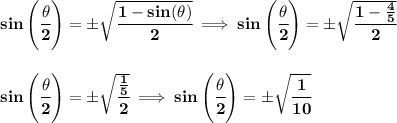
------------------------------------------------------------------------------------------
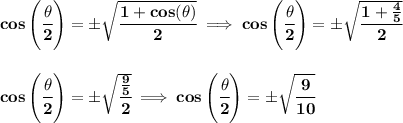
------------------------------------------------------------------------------------------