Question

Find the perimeter of the parallelogram. round to the nearest hundredths

Answer 1

Find the distance between the points of the parallelogram to find its sidelengths, then find the sum of these.

For AB and DC, there is no need to use any formula because both pairs are on the same y coordinate, which means that to find the distance between those points, it is only necessary to substract the x coordinates.

`\begin{gathered} 6-(-7)=13 \\ 4-(-9)=13 \end{gathered}`

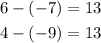
These sides measure 13 units.

For AD and BC it is necessary to use the following formula to find the distance between its points (you can only use one pair of points because AD and BC have the same lenght).

`\begin{gathered} d=\sqrt[]{(x2-x1)^2+(y2-y1)^2} \\ d=\sqrt[]{(6-4)^2+(5-(-2))^2} \\ d=\sqrt[]{2^2+7^2} \\ d=\sqrt[]{53} \\ d=7.28 \end{gathered}`

These sides measure 7.28 units.

To find the perimeter, add the sidelengths of the parallelogram, this way:

`\begin{gathered} P=13+13+7.28+7.28 \\ P=40.56 \end{gathered}`

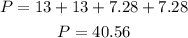
The perimeter of the parallelogram is 40.56,