Question

Two less than three times the width of a rectangle is equal to the length. The area of the rectangle is 65 square ft. What is the length of the rectangle? A) 9 feet B) 11 feet C) 13 feet D) 20 feet

Answer 1

c because 3 times the value.

Answer 2

Option C - 13 feet.

Explanation:

Given : Two less than three times the width of a rectangle is equal to the length. The area of the rectangle is 65 square ft.

To find : What is the length of the rectangle?

Solution :

The area of the rectangle is given by,

`\text{Area}=\text{Length}* \text{Width}`

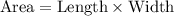
The area of the rectangle is 65 square ft.

Let the width of the rectangle be 'w'.

Two less than three times the width of a rectangle is equal to the length.

The length of the rectangle is l=3w-2

Substitute the value in the formula,

`65=(3w-2)* w`

`65=3w^2-2w`

`3w^2-2w-65=0`

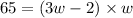
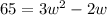
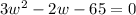
Applying quadratic formula,

`w=(-(-2)\pm√((-2)^2-4(3)(65)))/(2(3))`

`w=(2\pm√(4+780))/(6)`

`w=(2\pm√(784))/(6)`

`w=(2\pm28)/(6)`

`w=(2+28)/(6),(2-28)/(6)`

`w=(30)/(6),(-26)/(6)`

`w=5,-4.33`

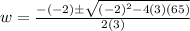
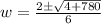
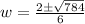
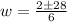
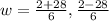
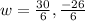
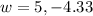
The width of the rectangle is 5 ft.

The length of the rectangle is l=3w-2=3(5)-2=13 ft

Therefore, Option C is correct.