7 bills of $5 and 20 bills of $10
Step-by-step explanation
Step 1
Let
Malick has $235=total = 235
total=235
number of bill $5= x
number of bill $10=y
He has one less than three times as many $10 bills than $5 bills=
3x=y+1
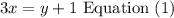
Step 2
the total is 235, so
total for $ 5 bills= 5* number of bills $5=5x
total for $ 10 bills= 10* number of bills $10=10x
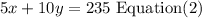
Step 2
using equation (1I and (2) solve for x and y
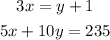
isolate, y in equation (1)
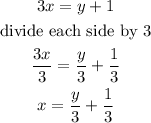
replace the value of x in equation (2)
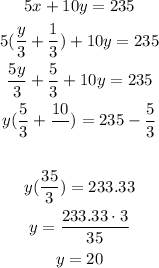
replace the value of y in equation (1) to fin d x
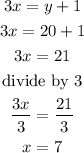
so, the answer is
7 bills of $5 and 20 bills of $10