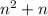We are asked to find the expression that can be used to determine the number of squares at stage n.
At stage 1:
There are 2 squares
At stage 2:
There are 6 squares
At stage 3:
There are 12 squares
At stage 4:
There are 20 squares
Substitute n = 1,2,3,4 into each option and check which option satisfies the above number of squares.
Option 1:
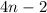
For n = 1:
4(1) - 2 = 4 - 2 = 2 (satisfied)
For n = 2:
4(2) - 2 = 8 - 2 = 6 (satisfied)
For n = 3:
4(3) - 2 = 12 - 2 = 10 (not satisfied)
Option 2:

For n = 1:
5(1) - 3 = 5 - 3 = 2 (satisfied)
For n = 2:
5(2) - 3 = 10 - 3 = 7 (not satisfied)
Option 3:
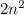
For n = 1:
2(1)^2 = 2(1) = 2 (satisfied)
For n = 2:
2(2)^2 = 2(4) = 8 (not satisfied)
Option 4:
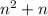
For n = 1:
(1)^2 + 1 = 1 + 1 = 2 (satisfied)
For n = 2:
(2)^2 + 2 = 4 + 2 = 6 (satisfied)
For n = 3:
(3)^2 + 3 = 9 + 3 = 12 (satisfied)
For n = 4:
(4)^2 + 4 = 16 + 4 = 20 (satisfied)
Therefore, the correct answer is option 4.
The following expression can be used to determine the number of squares at stage n.