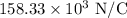Given:
The charge at x=0 is,
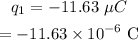
The other charge is,
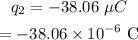
The second charge is at,
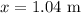
To find:
The electric field at,
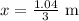
Step-by-step explanation:
The diagram of the charges is shown below:
The electric field at the given point due to the first charge is,
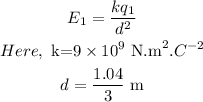
The electric field due to the first charge is,
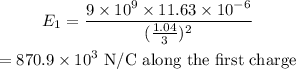
The electric field due to the second charge is,
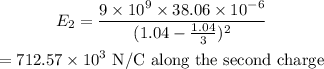
The electric fields are opposite each other. So, the net electric field is,
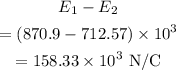
Hence, the magnitude of the electric field is