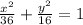Question

What is a standard form equation of the ellipse with verticals at (0,6) (0,-6) and co-verticales at (4,0) and (-4,0)?

Answer 1

Given:

The vertices of the ellipse are at (0,6) and (0,-6) and co-vertices at (4,0) and (-4,0).

Required:

We have to find the equation of the ellipse.

Step-by-step explanation:

The vertices are at (0,6) and (0,-6) then the length of the major axis is 6.

The co-vertices are at (4,0) and (-4,0) then the length of the minor axis is 4.

We know that the standard form of an ellipse is

`(x^2)/(a^2)+(y^2)/(b^2)=1`

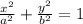
Where a and b are the length of the major axis and the minor axis respectively.

Then the required equation of the ellipse is

`\begin{gathered} (x^2)/(6^2)+(y^2)/(4^2)=1 \\ \\ \Rightarrow(x^2)/(36)+(y^2)/(16)=1 \end{gathered}`

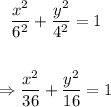
Final answer:

Hence the final answer is

`(x^2)/(36)+(y^2)/(16)=1`