Answer:
-$6.72
Explanation:
The cost of the ticket = $10
Let X be the possible profit on the ticket.
The probability distribution for X is given below.
Thus, the expected value for your profit is calculated below:
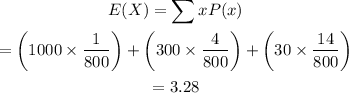
Subtract from 10:
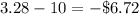
The expected value for your profit is -$6.72.
Note: This means that if you play the game, you expect to make a loss of $6.72 (rounded to the nearest cent).