Question

How many and of which kind of roots does the equation f(x) = x3 – x2 – x + 1 have?A. 2 real; 1 complexB. 1 real; 2 complexC. 3 realD. 3 complex

Answer 1

we have the equation

`f(x)=x^3-x^2-x+1`

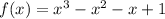
For x=1

f(x)=0

that means------> x=1 is a real root

Divide the given function by the factor (x-1)

x^3-x^2-x+1 : (x-1)

x^2-1

-x^3+x^2

-------------------

-x+1

x-1

---------

0

therefore

`x^3-x^2-x+1=\left(x-1\right)\left(x^2-1\right)`

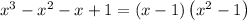
Solve the quadratic equation

`\begin{gathered} x^2-1=0 \\ x^2=1 \\ x=\pm1 \end{gathered}`

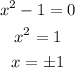
therefore

The equation has 3 real roots

Option C