Given:
650 lb of coffee is sold when the price is $4 per pound,
400 lb of coffee is sold at $8 per pound.
To find:
A) List the data points
B) The slope of line joining the points
C) Interpretation of meaning of slope of line
D) linear equation of data using point slope form
E) Using the function we need to predict the number of consumers buying at $6 per pound
Step-by-step solution:
A) Data points of the given data:
Data points:
(4,650) and (8,400)
B) The slope of the line joining the points:
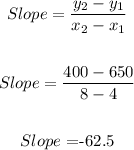
C) Interpretation of meaning of slope of line:
Slope here means that:
When there is an increase in the price of coffee then the weight of coffee decreases.
Weight per dollar of coffee decreases at the rate of 62.5
D) linear equation of data using the point-slope form:
Applying point-slope form:
y - y1 = m(x - x1)
y - 650 = -62.5(x - 4)
y = -62.5x + 900
In function notation it can be represented as:
S(P) = -62.5P + 900
E) Using the function we need to predict the number of consumers buying at $6 per pound
To predict that, we will simply put the value of P equal to 6 in the given function:
S(P) = -62.5P + 900 At P = 6
S(P) = -62.5(6) + 900
S(P) = 525
Thus we can say that 525 customers will buy at $6 per pound.