Question

Utopia Park has just installed acircular fountain 8 meters in diameter.The Park Committee wants to pave a1.5-meter-wide path around the fountain.If paving costs $10 per square meter, findthe cost to the nearest dollar of the pavedpath around the fountain.

Answer 1

Since the diameter of the circular fountain is 8m, then its radius is equal to 4m.

Since the path around the fountain will be 1.5 meters wide, then, the radius of the external circumference that determines the path around the fountan will be equal to 5.5 meters, as shown below:

The area that will be paved is equal to the difference between the area of the circle with a radius of 5.5m and the area of the circle with a radius of 4m.

The area of a circle with radius r is given by the expression:

`A=\pi r^2`

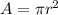
Replace r=4m to find the area of the fountain:

`A_{\text{fountain}}=\pi*(4m)^2=16\pi^{}\cdot m^2`

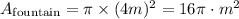
Replace r=5.5m to find the area of the fountain and the path:

`A_{\text{fountain}+\text{path}}=\pi(5.5m)^2=30.25\pi\cdot m^2`

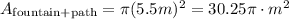
Substract the area of the fountain from the area of the fountain and the path to find the area of the path:

`\begin{gathered} A_{\text{path}}=A_{\text{fountain}+\text{path}}-A_{\text{fountain}} \\ =30.25\pi\cdot m^2-16\pi\cdot m^2 \\ =14.25\pi\cdot m^2 \end{gathered}`

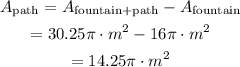
Since the cost to pave each square meter is $10, multiply the area of the path by 10 to find the cost of the paved path:

`10*14.25\pi=142.5\pi`

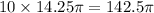
Find a decimal expression using the value of the constant π:

`\pi=3.141592653\ldots`

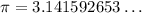
Then:

`142.5\pi=447.67695\ldots`

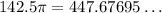
Therefore, to the neares dollar, the cost of the paved path around the fountain is: $448.