Question

Three vectors are shown in the figure. Their magnitudes aregiven in arbitrary units. Determine the sum of the three vectors.Give the resultant in terms of•components•magnitude•angle with the +x axis(Figure 1)

Answer 1

Components:

First, calculate the cartesian components of each vector, as follow:

`\begin{gathered} A_x=44.0\cdot\cos (28.0)=38.85 \\ A_y=44.0\cdot\sin (28.0)=20.65 \\ B_x=-26.5\cdot\cos (56.0)=-14.82 \\ B_y=26.5\cdot\sin (56.0)=21.97 \\ C_x=0 \\ C_y=-31.0 \end{gathered}`

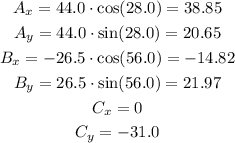
Next, consider that the components of the resultant vector R, are given by the sum of the x components and y components of all vectors A, B and C:

`\begin{gathered} R_x=A_x+B_x+C_x=38.5-14.82+0=23.68 \\ R_y=A_y+B_y+C_y=20.65+21.97-31.0=11.62 \end{gathered}`

Magnitude:

The magnitude is calculated as follow:

`R=\sqrt[]{R^2_x+R^2_y}=\sqrt[]{(23.68)^2+(11.62)^2}=26.38`

Angle with x axis:

The angle related to the x axis is obtained as follow:

The tangent of the angle related to the x axis is:

`\tan \theta=(R_y)/(R_x)`

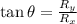
which is basically, the quotient between the opposite site and adjacent side of a right triangle formed by the components of the vector.

To obtain the angle you apply tan^-1 to cancel out the tangent, as follow:

`\theta=\tan ^(-1)((R_y)/(R_x))=\tan ^(-1)((11.62)/(23.68))=26.14\degree`