Question

A 1500 kg car on flat ground ismoving 5.25 m/s. Its enginecreates a 1250 N forward force asthe car moves 42.8 m. What is itsfinal velocity?(Unit = m/s)

Answer 1

From Newton's second law we know that:

`F=ma`

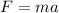
where F is the force, m is the mass and a is the acceleration. In this case the force exerted by the engine is 1250 N and the mass of the car is 1500 kg; plugging these values we have that:

`\begin{gathered} 1250=1500a \\ a=(1250)/(1500) \\ a=0.833 \end{gathered}`

Therefore, the acceleration of the car is 0.833 m/s².

From the previous result we notice that the acceleration is constant which means that the car will move in an uniformly accelerated motion which means that we can use the following equations:

`\begin{gathered} a=(v_f-v_0)/(t) \\ x=x_0+v_0t+(1)/(2)at^2 \\ v_f^2-v_0^2=2a(x-x_0) \end{gathered}`

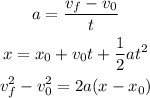
In this case we want to know the final velocity of the car after it moves 42.8 m and we know both the acceleration and the initial velocity (5.25 m/s); then we can use the last equation to determine it. Plugging the values we know and solving for the velocity we have:

`\begin{gathered} v_f^2-5.25^2=2(0.833)(42.8) \\ v_f^2=5.25^2+2(0.833)(42.8) \\ v_f=√(5.25^2+2(0.833)(42.8)) \\ v_f=9.94 \end{gathered}`

Therefore, the final velocity of the car is 9.94 m/s