Question

I have more information for the question I have more information if needed:Part 1)So it ask to find the probabilities that would be calculated in the labGroup of items: Deck of cardsCharacteristics of interest: Color of cardPossible outcome: Red face or Black faceNumber of items = 52 cards in a deckAction: A student can be asked to pick a random card from the deck of 52 cards and be required to find the probability of picking a black face.

Answer 1

Step-by-step explanation

In this probability exercise, we have a deck of 52 cards. Half of the cards are red, and the other half is black. We are interested in the probability of the following event: pick a black card.

1) Frequency table

To study the probability of this event. We perform the experiment of picking randomly a card from the deck and writing the result: B (black) or R (red). After that, we insert the card inside the deck. By repeating the experiment 50 times, we get the following table:

2) Probability model

A probability model is the mathematical representation of this experiment. It is defined by its sample space, events within the sample space, and probabilities associated with each event.

The elements of our model are:

• Sample space,: are the different cards of the deck, 26 Black and 26 Red:

• Events within the sample space,: pick a B (Black) card or R (Red) card.

,

• The probabilities associated with each event are,:

`\begin{gathered} P(B)=\frac{\text{\# of black cards}}{\text{ \# of cards in the deck}}=(26)/(52)=0.5, \\ P(R)=\frac{\text{\# of red cards}}{\text{\# of cards in the deck}}=(26)/(52)=0.5. \end{gathered}`

3) Verification

To verify the result of the experiment and the probability predicted by the mathematical model, we compute the quotient between the number of B (Black) cards obtained and the total number of trials:

`\text{ Experiment P\lparen B\rparen }=\frac{\text{\# of B cards}}{\text{ \# of trials}}=(29)/(50)=0.58.`

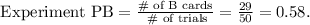
We see that the result differs from the probability predicted by the mathematical model. However, the experimental result of 0.58 is close to the one of the mathematical mode, 0.5. We expect that the numbers will coincide if we increase the number of trials.

Answer

1) Frequency table

2) Probability model

The elements of our model are:

• Sample space,: are the different cards of the deck, 26 Black and 26 Red:

,

• Events within the sample space,: pick a B (Black) card or R (Red) card.

,

• The probabilities associated with each event are,:

`\begin{gathered} P(B)=\frac{\text{\# of black cards}}{\text{ \# of cards in the deck}}=(26)/(52)=0.5, \\ P(R)=\frac{\text{\# of red cards}}{\text{\# of cards in the deck}}=(26)/(52)=0.5. \end{gathered}`

3) Verification

The experimental probability is:

`\text{ Experiment P\lparen B\rparen }=\frac{\text{\# of B cards}}{\text{ \# of trials}}=(29)/(50)=0.58.`

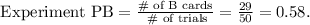
We see that the result differs from the probability predicted by the mathematical model. However, the experimental result of 0.58 is close to the one of the mathematical mode, 0.5. We expect that the numbers will coincide if we increase the number of trials.