Question

How many real number solutions does the equation have 0=5x^2+2x-12

A one solution
B two solutions
C infinitely many solutions
D no solutions

Answer 1

 Rearrange the equation to standard form of a quadratic equation (ax^2+bx+c=0) by switching sides: 5x^2+2x-12=0. Now, use the quadratic equation formula to solve. You should come out with x_1=sqrt61-1/5 and x_2=-1+sqrt61/5. Thus, your answer is B, or two solutions.

Answer 2

A. two solutions

Explanation:

To find the number of real solutions the equation is having, we need to solve first;

0=5x²+2x-12

This equation can be re-written as;

5x²+2x-12 = 0

We will use the formula method to solve

Using formula method;

x = -b ±√b² - 4ac / 2a

From the equation given,

a = 5 b = 2 and c=-12

x = -2 ± √2² - 4(5)(-12) / 2(5)

x = -2 ± √4 + 240 / 10

x = -2/10 ± √244 /10

x =
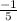`(-1)/(5)` ± 1.56

x = - 0.2 ± 1.56

Either x = -0.2 + 1.56 or x = -0.2 - 1.56

Either x = 1.36 or x = -1.76

Therfore, this equation have two real number solutions