Question

Suppose that CA = 12, CB = 20, DF = 6, and FE = 10. Which additional fact would guarantee that the triangles are SIMILAR?

Answer 1

It enough to show m∠C = m∠F to guarantee that the triangles are SIMILAR that is Δ ABC ≈ Δ DEF

Explanation:

Given : CA = 12, CB = 20, DF = 6, and FE = 10.

We have to find an additional fact that would guarantee that the triangles are SIMILAR that is Δ ABC ≈ Δ DEF

For two triangle to be similar when the ratio of their corresponding sides are same and measure of corresponding angles are equal.

Consider the Δ ABC and Δ DEF

Given CA = 12, CB = 20, DF = 6, and FE = 10.

Consider

`(CA)/(FD)=(CB)/(FD) \\\\\\(12)/(6)=(20)/(10)=(2)/(1)`

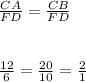
Since, ratio of two sides are in same ratio.

Thus, to have two triangles similar it is enough to show that the measure of angle between two sides must be same. by Side-angle-side similarity criterion.

That is m∠C = m∠F

Thus, it enough to show m∠C = m∠F to guarantee that the triangles are SIMILAR that is Δ ABC ≈ Δ DEF

Answer 2

m∠C = m∠F, There are different additional facts that would guarantee the triangles are similar. One is if you are told that the length of AB is twice the length of DE. Another is if angle C is congruent to angle F. You only need one of the two facts above. Are you given choices?