Answer:
It enough to show m∠C = m∠F to guarantee that the triangles are SIMILAR that is Δ ABC ≈ Δ DEF
Explanation:
Given : CA = 12, CB = 20, DF = 6, and FE = 10.
We have to find an additional fact that would guarantee that the triangles are SIMILAR that is Δ ABC ≈ Δ DEF
For two triangle to be similar when the ratio of their corresponding sides are same and measure of corresponding angles are equal.
Consider the Δ ABC and Δ DEF
Given CA = 12, CB = 20, DF = 6, and FE = 10.
Consider
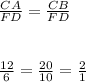
Since, ratio of two sides are in same ratio.
Thus, to have two triangles similar it is enough to show that the measure of angle between two sides must be same. by Side-angle-side similarity criterion.
That is m∠C = m∠F
Thus, it enough to show m∠C = m∠F to guarantee that the triangles are SIMILAR that is Δ ABC ≈ Δ DEF