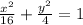Question

eliminate the parameter and write the corresponding rectangular equation whose graph represents the curve x=4costhetay=2sintheta

Answer 1

We have the following trigonometric identity:

`\cos ^2\theta+\sin ^2\theta=1`

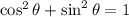
then, if we calculate the following expression:

`\begin{gathered} x^2+y^2=(4\cos \theta)^2+(2\sin \theta)^2 \\ =16\cos ^2\theta+4\sin ^2\theta \end{gathered}`

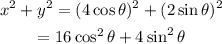
as we can see, the coefficients 16 and 4 gives us the lenght of the axis of the ellipse, therefore, the rectangular equation that eliminates the parameter is:

`(x^2)/(16)+(y^2)/(4)=1`