Question

For what value of n does 216^n-2/(1/36)^3n= 216

Answer 1

Option (d) is correct.

Explanation:

Answer 2

Option (d) is correct.

for n = 1
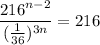`(216^(n-2))/(((1)/(36))^(3n) )=216` holds.

Explanation:

Given expression
`(216^(n-2))/(((1)/(36))^(3n) )=216`

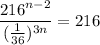
We have to find the value of n for which the given expression
`(216^(n-2))/(((1)/(36))^(3n) )=216`

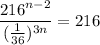
Consider the given expression
`(216^(n-2))/(((1)/(36))^(3n) )=216`

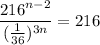
Apply exponent rule
`(1)/(a^b)=a^(-b)`

`(1)/(\left((1)/(36)\right)^(3n))=\left((1)/(36)\right)^(-3n)`

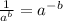
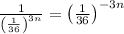
We get,

`216^(n-2)\left((1)/(36)\right)^(-3n)=216`

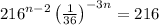
Convert
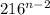`216^(n-2)` to base 6, we have
`216^(n-2)=\left(6^3\right)^(n-2)`

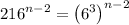
Thus, the expression becomes,

`\left(6^3\right)^(n-2)\left(6^(-2)\right)^(-3n)=216`

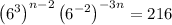
Apply exponent rule ,
`\left(a^b\right)^c=a^(bc)`

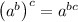
We get,

`6^(3\left(n-2\right))\cdot \:6^(-2\left(-3n\right))=6^(3\left(n-2\right)-2\left(-3n\right))`

`6^(3\left(n-2\right)-2\left(-3n\right))=216`

`\mathrm{If\:}a^(f\left(x\right))=a^(g\left(x\right))\mathrm{,\:then\:}f\left(x\right)=g\left(x\right)`

`3\left(n-2\right)-2\left(-3n\right)=3`

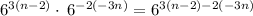
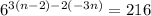
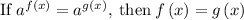
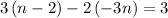
Simplify for n , we have,

n = 1

Thus for n = 1
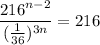`(216^(n-2))/(((1)/(36))^(3n) )=216` holds.