Question

I need step by step help with: 3x(x-1)^(1/3) + 2(x-1)^(3/2) = 0.

Answer 1

Hello ;
Let f be the function defined on [1; + infinite [such that for every x belonging to [1; + infinite [F (x) = 3x (x - 1) ^ (1/3) + 2 (x - 1) ^ (3/2).
We have: x> = 1 ==> x - 1> = 0> (x - 1) ^ (1/3)> = 0 ==> 3x (x - 1)> = 0.In the same way, we have: x> = 1 ==> x - 1> = 0 ==> (x - 1) ^ (3/2)> = 0 ==> 2 (x -1 )^3/2/> = 0.==> - 2(x - 1)^(3/2) =< 0 .
Hence: 3x (x - 1) ^ (1/3) +2 (x - 1) ^ (3/2) = 0= 3> (x - 1) ^ (1/3) = - 2 (x - 1) ^ (3/2) = <0
Therefore: 0 = <3x (x - 1) ^ (1/3) = <0Therefore: 3x (x - 1) ^ (1/3) = 0Thus (x - 1) ^ (1/3) = 0 (x can not be zero because x belongs to [1; + infinite [Therefore: x - 1 = 0Therefore: x = 1.

Answer 2

`3x(x-1)^(1/3)+2(x-1)^(3/2)=0`

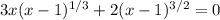
First note that, if you're solving over the real numbers only, the second term is defined for
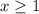
`x\ge1`, so any solution smaller than 1 will be considered extraneous (if we happen to find one).

Notice that if
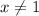
`x\\eq1`, you have the nontrivial task of finding roots (larger than 1 for the reason mentioned above) of a septic polynomial (degree 7):


`3x(x-1)^(1/3)+2(x-1)^(3/2)=0\iff-\frac32x=((x-1)^(3/2))/((x-1)^(1/3))=(x-1)^(7/6)`

`\implies\left(-\frac32x\right)^6=(x-1)^7\iff(729)/(64)x^6=(x-1)^7`

I'm afraid I can't be of any help there...

On the bright side, we can find at least one real solution:


`3x(x-1)^(1/3)+2(x-1)^(3/2)=(x-1)^(1/3)(3x+2(x-1)^(7/6))=0`

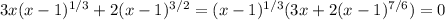
which admits at least that
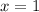
`x=1` is a solution to the equation.